Class X Session 2023-24 Question 8

 MATH SAMPLE QUESTION PAPER

Class X Session 2023-24

MATHEMATICS STANDARD (Code No.041) 

Question 8 

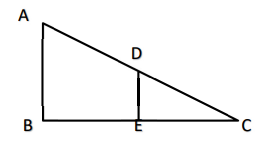
In 𝛥 ABC, DE ‖ AB. If AB = a, DE = x, BE = b and EC = c Then x expressed in terms of a, b and c is:

\begin{flalign} (a)\;\;& \frac{ac}{b}\\ (b)\;\;& \frac{ac}{b+c} \\ (c)\;\;& \frac{ab}{c}\\ (d)\;\;& \frac{ab}{b+c}&\\ \end{flalign}

Explanation : 

\begin{flalign} Since \; DE\;&\Vert \; AB \; we \;can \;similar \; \triangle \; find \;the\; length&\\ \end{flalign}

Using the properties of basic proportionality theorem we have 

\begin{flalign} &\triangle \; CDE \; \sim \; \triangle \; CAB \ \end{flalign}

\[\Rightarrow \; \frac{CE}{CB} =\frac{DE}{AB}\]

\[OR \; \frac{CE}{BE + EC} =\frac{DE}{AB}\]

\[\Rightarrow \; \frac{c}{b+c} =\frac{x}{a}\]

\[OR \; \; {x} =\frac{ac}{b+c}\;...by \; cross \; multiplication\]

 

Guess the Option and comment below  👇