Class X Session 2023-24 Question 21

 MATH SAMPLE QUESTION PAPER

Class X Session 2023-24

MATHEMATICS STANDARD (Code No.041)

SECTION B - Question 21

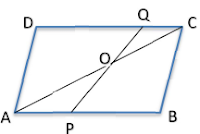
ABCD is a parallelogram. Point P divides AB in the ratio 2:3 and point Q divides DC in the ratio 4:1. Prove that OC is half of OA.

Explanation :

ABCD is a parallelogram.

we know that AB = DC

let AB = l

then AB = DC = l

given that Point P divides AB in the ratio 2:3

\[\Rightarrow AP = \frac{2}{5}\times l;and\;BP \;=\frac{3}{5}\times l \]

\[Since\; we \;considered\; AP + BP = AB = l \]

\[\Rightarrow DQ = \frac{4}{5}\times l;and\;CQ \;=\frac{1}{5}\times l \]

given that point Q divides DC in the ratio 4:1

\[Since \; DQ + CQ = DC= l \]

As we know that [AA similarity]

\[\therefore ∆ APO \thicksim ∆ CQO \]

\[\therefore \frac{AP}{CQ} = \frac{PO}{QO} = \frac{AO}{CO} \]

\[\therefore \frac{AO}{CO} = \frac{\frac{2}{5}\times l}{\frac{1}{5}\times l} = \frac{2}{1} \]

After simplifying the above equation, we get

\[\Rightarrow OC = \frac{1}{2} \times AO \]