Class X Session 2023-24 Question 16

 MATH SAMPLE QUESTION PAPER

Class X Session 2023-24

MATHEMATICS STANDARD (Code No.041)

Question 16

There is a square board of side ‘2a’ units circumscribing a red circle. Jayadev is asked to keep a dot on the above said board. The probability that he keeps the dot on the shaded region is.

$$\begin{array}{rl}(a)& \frac{\pi }{4}\\ (b)& \frac{4-\pi }{4}& & \\ (c)& \frac{\pi -4}{4}& & \\ (d)& \frac{4}{\pi }& & \end{array}$$

Explanation : 

Given that ,

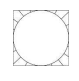
The square board has side length 2a units and the board circumscribes a red circle. The shaded region represents the area within the square board but outside the red circle.

so we have to find the ratio of the area of the shaded region to the total area of the square board.

we know that area of the square is side^2 

=> 4a^2 square units.

similarly 

area of the red circle  

=> π(radius)^2 = π(a)^2

$$\therefore Areaofshadedregion=4a^2-\pi (a{)}^{2}squareunits$$

The probability that Jayadev keeps the dot on the shaded region is the ratio of the area of the shaded region to the total area of the square board

$$Probability=\frac{Areaofsquare-Areaofcircle}{Areaofsquare}=\frac{\sqrt{(4-\pi )a^2}}{4a^2}$$

$$Probability=1-\frac{\pi }{4}$$

Guess the Option and comment below  👇