Class X Session 2023-24 Question 20
MATH SAMPLE QUESTION PAPER
Class X Session 2023-24
MATHEMATICS STANDARD (Code No.041)
Question 20
\begin{flalign}
& Statement A (Assertion )\; 5,\; \frac{-5}{2},\; 0,\; \frac{5}{2} …. \;is\; in \;Arithmetic\; Progression.&\\
\end{flalign}
Statement R (Reason) : The terms of an Arithmetic Progression cannot have both positive
and negative rational numbers.
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation
of assertion (A)
(b) Both assertion (A) and reason (R) are true and reason (R) is not the correct
explanation of assertion (A)
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.
Explanation: let's understand the AP
where AP is a sequence of numbers in order, in which the difference between any two consecutive numbers is a constant value.
The general form of an arithmetic progression is a , a+d,a+2d,a+3d,…
where
a is the first term .
d is the common difference between terms.
a+nd represents the nth term of the sequence.
below is the example of AP with +3 common difference -
Now come to the question, The correct option is (a)
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A)
Statement A (Assertion) is true
\begin{flalign}
& Statement A (Assertion )\; 5,\; \frac{-5}{2},\; 0,\; \frac{5}{2} …. \;is\; in \;Arithmetic\; Progression.&\\
\end{flalign}
is indeed an arithmetic progression because the difference between consecutive terms is constant. In this case, the common difference is
\begin{flalign}
& \frac{-5}{2} - 5 = \; \frac{15}{2}\;&\\
\end{flalign}
Statement R (Reason) is also true. In an arithmetic progression, the terms usually have a consistent direction (either all positive or all negative) or are all integers or fractions of the same sign. It's rare for an arithmetic progression to contain both positive and negative rational numbers. Therefore, the reason correctly explains why such a sequence would not typically be considered an arithmetic progression
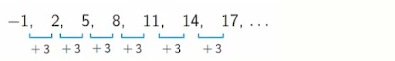
Comments
Post a Comment