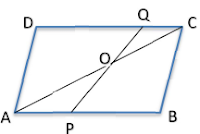
Class X Session 2023-24 Question 26

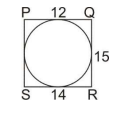
MATH SAMPLE QUESTION PAPER Class X Session 2023-24 MATHEMATICS STANDARD (Code No.041) Question 26 Find the area of the unshaded region shown in the given figure. Solution: modified view of shared image The total horizontal or vertical extent of the region is 8 cm and extent includes the side length of the square (𝑎) and the diameters of the semicircles on either side of the square. Given that each semicircle has a radius 𝑟, the side length of the square is 𝑎=8−2𝑟. Given the figure, the radius 𝑟 of each semicircle is 2cm Side Length of the Square 𝑎 = 8-2x2 = 4 cm Area of the Square: 𝑎^2 = 4^2 = 16 Area of One Semicircle = \[ \frac{1}{2} {\pi} r^2 = 2{\pi} \; cm^2\; where \; r= 2 \] Combined Area of Four Semicircles: \[4\times 2\pi\; cm^2\] Area of the unshaded region=Area of the square + 4 x Area of one semicircle = \[16 \; cm^2 + 4 \times2 {\pi} \; cm^2 \] \[(\;16 + 8{\pi}\;) \; cm^2\]