Class X Session 2023-24 Question 3
MATH SAMPLE QUESTION PAPER
Class X Session 2023-24
MATHEMATICS STANDARD (Code No.041)
Question 3
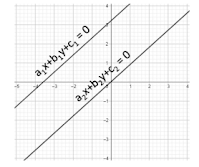
The lines representing the given pair of linear equations are non-intersecting. Which of the
following statements is true?
\begin{flalign} (a)\;\;& \frac{a1}{a2} =\frac{b1}{b2} =\frac{c1}{c2}&\\ (b)\;\;& \frac{a1}{a2} =\frac{b1}{b2} \neq\frac{c1}{c2}&\\ (c)\;\;& \frac{a1}{a2} \neq\frac{b1}{b2} =\frac{c1}{c2}&\\ (d)\;\;& \frac{a1}{a2} \neq\frac{b1}{b2} \neq\frac{c1}{c2}&\\ \end{flalign}Explanation :
Let us examine each choice and determine the right response.
\[(a) \ \ \frac{a1}{a2} = \frac{b1}{b2} = \frac{c1}{c2} \]
This option suggests that the ratios of the coefficients for x and y and the constant terms in the two equations are all equal . In terms of slopes, it implies that the slopes of the two lines are equal.
Additionally, it suggests that the lines pass through the same point on the y-axis. This option is not correct.
\[(b) \ \ \frac{a1}{a2} \ = \frac{b1}{b2} \ \neq \frac{c1}{c2} \] --Correct Ans
\begin{flalign} & \frac{a1}{a2} =\frac{b1}{b2}:&\\ \end{flalign}
This part implies that the slopes of the two lines are equal. This suggests that the lines have the same steepness.
\begin{flalign} & \neq \frac{c1}{c2}:&\\ \end{flalign}
This part indicates that the constant terms (y-intercepts) of the two lines are not equal. This means that the lines do not pass through the same point on the y-axis.
Putting it together, option (b) describes a situation where the slopes of the two lines are equal, indicating that these lines have the same steepness, but they do not pass through the same point on the y-axis. This scenario is consistent with the condition of non-intersecting lines.
\[(c) \ \ \frac{a1}{a2} \neq \frac{b1}{b2} \ = \frac{c1}{c2} \]
This option suggests that the slopes of the two lines are not equal, but the constant terms (y-intercepts) are equal. In other words, the lines have different steepness, but they pass through the same point on the y-axis. - Not correct
\[(d) \ \ \frac{a1}{a2} \neq \frac{b1}{b2} \ \neq \frac{c1}{c2} \]
This option suggests that none of the ratios of coefficients are equal. In other words, the slopes of the lines are all different, and the constant terms (y-intercepts) are also different. - Not correct
Guess the Option and comment below 👇
Comments
Post a Comment